|
I discovered the late-night radio talk show Loveline, with Adam Carolla and Dr. Drew Pinsky, just before Christmas 1999. I was in eighth grade and starting to assert personal independence. With the benefit of hindsight, it's difficult to overestimate how important that discovery was because hearing frank and explicit discussion of sexual matters helped me realize, understand, and accept my own maturation process, both physical and mental. I suspect I'd be a very different person today had I not randomly encountered that broadcast while scanning the radio dial that night. Like many adolescents, I used musical preference as a way to establish an identity, or at least the beginnings of an adult identify. I suspect many of a certain age connect The Beatles with this process, one major reason they're still so popular a half-century later. And Loveline would frequently feature guests, including many pop bands who were promoting their recent records. One night, I turned on the radio and heard for the first time a band called Stone Temple Pilots. They played a song called 'Sour Girl' from their 1999 album No. 4, which immediately captivated my 14-year-old ears. Fast forward 19 years, and I've forgotten about 'Sour Girl' - but not about Loveline. A while back, I discovered the website www.lovelinetapes.com, which contains exhaustive archives of Loveline shows. In a nostalgic bid, I decided to listen to the entire archive in chronological order. And the other night I stumbled upon that same broadcast with STP that I heard two decades ago, including its performance of 'Sour Girl' (and now I even know the exact date: 10 May 2000). This time, my musically-trained 33-year-old ears heard all sorts of new and fascinating musical subtleties that my eighth-grade ears were too inexperienced to notice. And so I set out to analyze it. Here's a transcription:
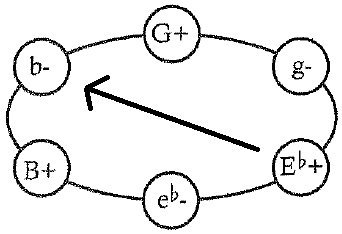
One of the first things I noticed was the change in key between the verse and chorus. The former seems to be in D major while the latter is in C major. What particularly captures my current attention is Robert DeLeo's bass line, which, by often playing the third and fifth of the tonic D major chord, constantly undermines any authoritative tonal conclusions about the verse. This is an example of what Mark Spicer calls a "fragile tonic", in which “the tonic chord is present but its hierarchical status is weakened." DeLeo's bass line is also what determines the BbMM7 chord (bVI in D) that appears near the end of each verse, differentiating that particular progression from the D minor chord that appears earlier in the same location. By altering the bass line, DeLeo also alters the progression, changing things up to keep a listener engaged. Even more fascinating is the harmony. That BbMM7 chord in the verses foreshadows the Bb that initiates the chorus. This time, however, because of the key change to C major, Bb is now bVII instead of bVI. While Bb moves to F in both the verse (bVI-bIII) and chorus (bVII-IV), in the verses that F proceeds to G (IV), while in the chorus it resolves to C (I). It's a great example of what I call "multifunctional harmony", where the same chords can function in different ways, even within the same song. Lastly, and most important, the harmony is also heavily chromatic. The intro riff and chords employ 10 of the 12 tones (only C# and G# are absent). While the progressions from F-C and C-G are extremely common, the move from Eb major to B minor is striking and most unusual. This is what Richard Cohn calls a "hexatonic pole" because it jumps across the hextonic cycle - in other words, it's as far away as you can get and still be in the same hexatonic cycle (Cohn, p. 18). Hexatonic poles are exceedingly rare in pop music - I cannot think of any examples. The closest I can think of is The Beatles' 'Michelle', which uses a similar but not identical progression from Eb6 (Eb-G-Bb-C) to B°7 (B-D-F-Ab). So 'Sour Girl' is, at least to my knowledge, the first pop song to employ a hexatonic pole.
REFERENCES Cohn, Richard. 2012. Audacious Euphony. Oxford University Press.
6 Comments
Common-practice functional harmony is predicated on the progression from predominant to dominant to tonic. In the below example of Mozart's Piano Sonata No. 13, those functions are abbreviated by their initial. Like classical harmony, pop harmony is also functional in the sense that certain chords lead to other chords, usually culminating in a cadence. However, unlike classical music, pop chords are subject to far less strict rules of progression. In other words, the progressions found in pop music are more flexible than those found in classical, with the same chords (or at least the same Roman Numerals) functioning in multiple ways. And that means any theory of popular music harmony must account for this multifunctional flexibility. Enter Christopher Doll. In his book Hearing Harmony (University of Michigan Press, 2017), Doll implements Greek letters to indicate distance from tonic:
Doll goes into some depth in an appendix, specifying all possible chords in each of these functions and providing names like "hypo pre-subdominant (mediant of a subdominant)" and "medial pre-dominant (mediant of a dominant)". While I appreciate the thoroughness of his theorizing, I find the exhaustive details cumbersome to the point of being unusable in practice. But I find his notion of Greek letter functions quite compelling and practical. Applying Doll's Greek letters to the same Mozart example shown above yields the following: In this case, ii (c) functions as the predominant (γ), V7 (F7) as dominant (β), and I (Bb) as tonic (α). It's a straight-forward, textbook example. But what about a pop song, such as Alanis Morissette's 'You Oughta Know'? Here's the chorus from that song, which clearly employs functional chord progressions but in a rather different way from Mozart: In this case, IV (B) is the pretonic chord (β). It resolves to I (α) on the subsequent downbeat. bIII (A), then, is the pre-pretonic (γ); and bVII (E) the pre-prepretonic (δ). But that is just one example. What makes these Greek letter functions so compelling and useful is how flexible they are. The same chords can function in different ways depending on their syntactical order. Here is the chorus from Metallica's 'The Unforgiven', which incorporates similar chords but with different functions: This time i (a) is α, V (e) is β, bVII (G) is γ, and bIII (C) is δ. To avoid constantly scrolling up and down to compare the two songs, here are the Greek letter functions of both 'You Oughta Know' and 'The Unforgiven' side-by-side:
Tonic, whether major (I) or minor (i), will always be α - that will not change from one progression to another. But all other Greek functions are liable to change. Notice how β is IV in one song but V in the other. And how both bIII and bVII are γ in one but δ in the other. This is what I mean when I say pop harmony is multifunctional - the same chords can function in different ways. This is contrast to classical harmony, where chords typically function one way, and only one way. The value of Christopher Doll's Greek letter functional nomenclature, then, is that it addresses pop music's more flexible rules of progression - it illustrates the linear harmonic motion without the restrictive and loaded terminology of classical analysis.
In 1975, Pink Floyd released what I consider to be their best album, Wish You Were Here. The album consists of five tracks:
Despite its seven-and-a-half-minute length, 'Welcome to the Machine' employs only four chords: E minor, C major, A minor, and A major. Of those four, the A major might be the most curious because it is heard only once (during the second verse, at 4:18), where it substitutes for the A minor chord heard during the initial verse. The obvious question, then, is why? Why does the second verse use an A major chord where the first verse uses an A minor? What is the point of making that substitution? Before we can answer that question, we first need to progress to the next track.
Like its immediate predecessor, 'Have A Cigar' also uses only four chords: E minor, C major, D major, and G major. Notice that two of these four chords (E minor and C major) were used in 'Machine', while the other two (D major and G major) were not.
So we have seen how 'Machine' uses the chords E minor, C major, A minor, and A major, and how 'Cigar' uses E minor, C major, D major, and G major. Now, given the title of this blog, can you make an educated guess regarding what chords are used in the title track? I'll give you a hint: There are six of them. Those six chords are E minor, C major, A minor, A major, D major, and G major. They should be very familiar since they are the combined harmonies from the two previous tracks - no more, no less. This is what I mean by the term "chordal accretion". Here's the same concept using color-coded mathematical symbols: The chords of 'Welcome to the Machine' (E minor, C major, A minor, A major) + The chords of 'Have A Cigar' (E minor, C major, D major, G major) = The chords of 'Wish You Were Here' (E minor, C major, A minor, A major, D major, G major)
So, getting back to that curious A major chord in 'Welcome to the Machine', the reason it's an A major in the second verse instead of A minor is to help set up this chordal accretion process, which culminates in the focal point of the entire album, the title track.
Many people have asked me about the band Cheap Trick, and they are mildly shocked when I say I'm not at all familiar. “They're so similar to The Beatles,” they enthuse, “you'd love them!” So the other day I listened to their self-titled 1977 debut album. And indeed they are similar to The Beatles! With this post, I'm launching a blog series on the comparison, starting with 'Mandocello', the ninth track of Cheap Trick. Here's a structural analysis and transcription: 0:00 Instrumental Intro 0:21 Riff and groove established 0:31 Verse 1 ("I can hear you laughing") 0:48 Verse 2 ("I will never leave you") 1:05 Instrumental Break 1:19 Verse 3 ("the thoughts you're thinking") 1:37 Verse 4 ("I can see you crying") 1:53 Abbreviated Instrumental Break 2:02 Bridge ("Look at me") 2:39 Abbreviated Verse 5 ("I can hear you thinking") 2:52 Verse 6 ("I'm the dream you're dreaming") 3:09 Terminus ("We can go down slowly") 3:37 Guitar Solo 3:47 Concluding Instrumental Verse 4:14 Instrumental Coda
The first similarity I hear to a Beatles song is in the intro (and coda), where a C major chord (shown in red in the graphic below) moves to a CMM7 (shown in blue). This progression is heard four times in 'Mandocello' - twice during the intro and twice more during the coda. It's a pattern that has been used many times in other songs, including in the verses of George Harrison's 'Something'. Second, there is another similarity to 'Something': The first instrumental break of 'Mandocello' incorporates the peculiar progression Eb-G-C (bIII-V-I in C major), which is nearly identical to the famous opening riff in 'Something'. Third and most significantly, each verse of 'Mandocello' features a syncopated 5/4 bar (transformed into a 12/8 bar during the instrumental concluding verse) with a descending bass pattern and arpeggios... ...which bears a striking resemblance to Harrison's other song on Abbey Road, 'Here Comes the Sun'. Fourth and least significantly, the bridge of 'Mandocello' opens with the lyrics "look at me", which, coincidentally or otherwise, is also the title of a John Lennon song written in 1968 but not released until 1970 on his debut solo album John Lennon/Plastic Ono Band. The similarities, though modest, are still present - similar melodic contours and lyrical content. Given how familiar Cheap Trick was with The Beatles' output, it seems too close to be coincidence. I'm guessing this is conscious on Cheap Trick's part. Fifth and lastly, this "look at me" bridge employs progressive extended tertian vocal harmonies. The first phrase extends only to the 3rd and 5th; the second and third phrases extend to the 7th and 9th; and the fourth and climactic phrase of the section extends to the 11th and 13th. While not common, extended tertian vocal harmonies are significant in Beatles music, too. A good example can be heard in their 1965 song 'Ticket to Ride', which similarly builds up to a 7th and 9th above the root. So there are my thoughts on Cheap Trick's 'Mandocello'. I look forward to writing additional blogs comparing and contrasting with The Beatles as I listen through Cheap Trick's catalog.
I've never been a big fan of the band Kiss, but yesterday I discovered a peculiar use of asymmetric rhymes in their hit "C'mon and Love Me", from their 1975 album Dressed to Kill. First, here's a basic formal and choral analysis, plus a PDF transcription: 0:00 Intro C5(2) Ab5(2) C5(2) Ab5(2) 0:14 Verse 1 C5(4) Ab5(1) Bb5(1) C5(2) 0:29 Verse 2 C5(4) Ab5(1) Bb5(1) C5(2) 0:44 Chorus Eb5(2) Bb5(2) Eb5(2) F5(1) G5(1) C5(2) Ab5(2) 1:06 Verse 3 C5(4) Ab5(1) Bb5(1) C5(2) 1:21 Verse 4 C5(4) Ab5(1) Bb5(1) C5(2) 1:35 Chorus Eb5(2) Bb5(2) Eb5(2) F5(1) G5(1) C5(2) Ab5(2) 1:51 Solo C5(1) Ab5(½) Bb5(½) C5(1) Ab5(½) Bb5(½) C5(1) Ab5(½) Bb5(½) C5(1) Bb5(1) 2:05 Chorus Eb5(2) Bb5(2) Eb5(2) F5(1) G5(1) C5(2) Ab5(2) 2:20 Coda C5(1) Ab5(½) Bb5(½) repeat and fade
The first thing that caught my attention was the chorus, which employs hypermetric asymmetric rhymes. In the first line, the syllable "tate" from "hesitate" rhymes with "wait"; in the second line, "knees" rhymes with "please". All four syllables occur essentially on beat 3 of their measures (more precisely the & of 2). But "tate" and "knees" (highlighted in blue) fall on even-numbered measures (two and six, respectively), while their rhyming counterparts "wait" and "please" (highlighted in red) fall on odd-numbered measures (three and seven). This discrepancy results in hypermetric asymmetric rhymes. It's as if the music is too impatient to rhyme on hypermetrically symmetric measures (two rhymes with four; six with eight), which reflects the "don't hesitate cuz I just can't wait" lyrics. Interestingly, the verses also incorporate asymmetric rhymes, though in less obvious and less consistent ways. Each of the four verses rhymes on the downbeats of the even measures (verse 1: romancer/cancer, verse 2: get me/let me, verse 3: baby/lady, verse 4: nearer/mirror), all shown in blue. But notice how verses 1 and 2 also rhyme on the downbeat of the first full measure (verse 1: dancer, verse 2: met me), shown in light blue, also resulting in hypermetric asymmetry. These additional rhymes conspicuously disappear in the third and fourth verses. Why? The first and second verses (0:14 and 0:29) are both heard BEFORE the first chorus (0:44), while the third and fourth verses (1:06 and 1:21) are both heard AFTER. So the additional rhymes in the initial two verses foreshadow the hypermetric asymmetry of the chorus. And once the chorus has been heard, there is no need to continue foreshadowing it in the subsequent verses.
Most pop music lyrics rhyme. And most of those rhymes are symmetric, meaning the rhymed syllables fall on the same rhythmic beat of different measures. Take, for example, the first verse (0:12-0:32) of Maren Morris' 2016 hit '80s Mercedes': In the first line she rhymes "last" with "dash", and in the second line she rhymes "practicality" with "me". All rhyming syllables are on the fourth beats of their measures (highlighted in red). This rhythmic consistency makes the rhymes symmetric. But some songs break this pattern. The choruses of Madonna's 'Material Girl', for example, rhyme "world" with "girl", but the former is heard just before beat 3 (red) while the latter is heard just before beat 1 (blue). This lack of rhythmic consistency makes the rhymes asymmetric. A more unusual example is Bon Jovi's 'You Give Love A Bad Name'. This time the syllable heard first on beat 3 ("blame" in red) is paired with the rhyming syllable on beat 2 ("name" in blue). The shift from beat 3 to beat 2 yields a displacement of one beat - unlike the 'Material Girl' example above, which pairs beats 3 and 1, a displacement of two beats, which is much more common. One of the things that makes 'Bad Name' a particularly interesting example is that the lead guitar, which obviously can't sing lyrics, retains this asymmetry in the introduction (0:13-0:20). This proves that music doesn't necessarily need rhymes to employ asymmetry. It's just most common and most noticeable though lyrics. For some reason - I have yet to pinpoint why - asymmetric rhymes seem to be most common in country styles. As a mandolin player, I'm quite fond of bluegrass, and Harley Allen and Mike Lilly's 'Suzanne' employs asymmetric rhymes in both the verses and choruses, each using the more conventional pairings of beats 3 (red) and 1 (blue). Another conventional 3-to-1 country example is found in The Nitty Gritty Dirt Band's 'Baby's Got A Hold On Me': Since asymmetric rhymes are more of a rhythmic device than a lyrical one, musicians could easily employ the same trick but on a deeper, hypermetric level. Indeed, hypermetric asymmetric rhymes can be heard in my opening example, '80s Mercedes'. The verses, as described above, use two-bar phrases with symmetric rhymes on the fourth beat of the first measures. But the prechorus speeds things up to a single measure.
The prechoruses rhyme "go" and "soul" just before beat 4 (in red). While these are still symmetric because each rhyme is on the same beat within the measure, the hypermetric quickening gives the impression of asymmetry in this specific context. However, in the last measure of the prechorus, she stutters, putting "go" just before beat 2 (in blue). And that is true asymmetric rhyming. Yesterday, while walking my puppy dog, I did what I always do: put in ear phones. I started with the audio book A Generation of Sociopaths: How the Baby Boomers Betrayed America by Bruce Cannon Gibney, but when that proved too depressing, I switched to music. A few days ago my wife commented on how she liked Ariana Grande's voice, so when I saw Grande's 2014 album My Everything in my library, I gave it a go. The first track, appropriately titled 'Intro', immediately captured my attention. First, a full structural analysis: 0:00-0:22 (A) Instrumental Introductory Verse (8) (a) statement (2) Cb | Gb (a) restatement (2) Cb | Gb (b) departure (2) Fb2 Cb/Eb | Gb/Db CØ7 (c) conclusion (2) Cb | Db4-3 0:22-0:43 (A) Verse 1 (8) (a) statement (2) Cb | Gb "I'll give..." (a) restatement (2) Cb | Gb "Love me..." (b) departure (2) Fb2 Cb/Eb | Gb/Db CØ7 "road to the sky..." (c) conclusion (2) Cb | Db4-3 "I promise you..." 0:43-1:05 (A) Instrumental Solo (8) (a) statement (2) Cb | Gb (a) restatement (2) Cb | Gb (b) departure (2) Fb2 Cb/Eb | Gb/Db CØ7 (c) conclusion (2) Cb | Db4-3 1:05-1:19 (A') Instrumental Coda (4) (a) statement (2) Cb | Gb (a) restatement (2) Cb | Gb Each section is fundamentally the same, despite surface-level differences, rendering the structure a Simple (or Strophic) design. The coda, though related, is clearly supplemental to the form because its abbreviated. You could argue that the intro is also supplemental (introductions are by definition supplemental), yielding an A x2 with intro and coda; however, since the intro is a full iteration of the module, I would count it as the first A section, making it an A x3 with coda. Either interpretation works, but I find the latter more accurate. That being said, it's not quite as straightforward as it might appear because Grande plays with the phrase rhythms during the solo. While the underlying harmonies retain the same two-measure hypermetric phrasing as the rest of the song, the melodic instrumental phrasing of the solo (starting in bar 17) through the coda is offset by one measure. This creates a greater sense of finality at the song's end by giving the impression of concluding on a hypermetrically strong beat, even though it's actually a weak beat. This is brilliant songwriting! Even more fascinating are the chords. Each departure phrase halves the harmonic rhythm, fitting two chords per bar (one chord every two beats, for a total of four chords in two measures), where the other phrases employ just one chord per bar (one chord every four beats, for a total of two chords in two measures). The fourth of those four departure phrase chords is the most unusual and interesting: It's a C half-diminished seventh (C-Eb-Gb-Bb). Half-diminished sevenths are rare in popular music. The Beatles used them in only two of their 211-song official catalog: 'Because' and 'You Never Give Me Your Money' (curiously, one Lennon song and one McCartney song, both from 1969's Abbey Road). No doubt there are other pop songs that employ this rare and intriguing harmony, but I can't think of any off the top of my head. Anyway, Ariana uses the half-diminished seventh somewhat differently than did John and Paul. (I don't know enough about Grande to know if she's a composer as well as a singer, but for the sake of this blog I will assume she is.) All three songwriters use the chord as a pre-dominant, but where The Beatles always employ it as a ii chord, Grande's use of the same harmony is not so evident. This ambiguity stems from the fact that it's almost several other chords, but not quite. Interpretation One: vi/#4 At its simplest, it could be interpreted as a conventional vi chord, but with a #4 (or b5) in the bass. This would render the progression (technically a retrogression) as bVII-IV-I-vi (in Gb: Fb-Cb-Gb-eb), which appears totally reasonable to the eye, though I can't think of any other song to use that particular pattern in a single phrase. (The Beatles used it in 'Dig A Pony', but as incongruent constituents bridging two consecutive phrases.) The problem is I just don't hear it that way. In other words, yes, this interpretation looks good, but I don't think it accurately captures what I'm hearing. Interpretation Two: augmented sixth What I'm hearing, that the above interpretation neglects, is how the C and Bb function like an augmented sixth chord. Enharmonically reinterpreting the C as Dbb gives it properly spelled augmented sixth function, as it resolves by half step down to Cb (shown in blue in the example below), just as the Bb resolves up to the same pitch class (shown in red). Okay, so now it does reflect what I'm hearing. But this "fix" creates a few new complications:
Interpretation Three: CTØ7 Common tone diminished chords are standard - they're a staple of romantic and barbershop styles. So could this mystery chord in 'Intro' be one? I have two problems with that notion. First of all, common tone diminished chords are usually common tone fully diminished seventh chords, where this would be a common tone half-diminished seventh - something I've never encountered before in any style or context. And second, common tone diminished chords are "supposed" to keep the root as the common tone, where in this case the third and the fifth are common tones while the root is not. So, technically, yes, this is a common tone diminished - it's just not what music theorists normally mean when they use that term. The bottom line is: I have no idea how to interpret this chord. And that ambiguity makes for absolutely fascinating and engaging analysis and consideration.
In the face of all this ambiguity, it's difficult - maybe even impossible - to make any clear verdicts. Yet I can draw one conclusion with utmost certainty: I'll be listening to a lot more Ariana Grande! Trevor de Clercq, Assistant Professor in the Recording Industry faculty at Middle Tennessee State University, authored an article titled "Measuring a Measure: Absolute Time as a Factor in Determining Bar Lengths and Meter in Pop/Rock Music" in 2016. This blog is a summary and critique of that article. The article opens with three different transcriptions of The Beatles' 1966 'Norwegian Wood (This Bird Has Flown)'. To be clear, they are all correct, even thought they all employ different time signatures. Had The Beatles written down their songs as sheet music, we could use whatever meter that sheet music used as the definitive interpretations. However, with no such "official score" available, de Clercq ponders, "Is one of these time signatures more appropriate than the others?" And to answer that question, he posits "that absolute time plays a significant role in determining our perception of meter". He further suggests that "about two seconds" is the best ballpark absolute duration per measure. In other words, if you have to chose between multiple valid options for an ambiguous meter, your default interpretation should be that which is closest to two seconds, which he considers the Goldilocks zone: not too short, not too long, but just right. Applying that principle to 'Norwegian Wood', the best choice would be 6/8, which, at 60 bpm, yields precisely two seconds per measure. Having objectively summarized de Clercq's main point (the "two second rule"), I'll now subjectively critique the essay. To do so, I will distinguish between the content of the article and the presentation of that content.
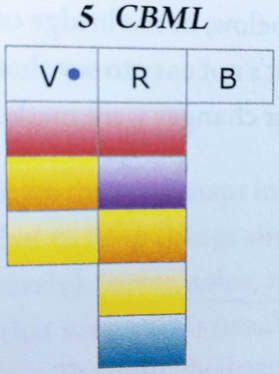
The content - mainly that two seconds per measure should be the default duration when transcribing rock music - I find valid and compelling. I will certainly adopt this "two second rule" whenever I'm analyzing pop music in the future. That being said, I find the same problem I often encounter in academic essays in the presentation - mainly that it's too long and too complicated. I'm a firm proponent of the "less is more" writing philosophy - that authors should write only enough to effectively articulate their meaning because writing any more than that is superfluous! But the academic approach to writing, as witnessed in this essay, seems to be "why write three pages when you could write forty pages saying the same thing?" This is overly-formal, meaning it's formal to the point of inhibiting understanding. And as professional educators, aren't academics supposed to facilitate learning, rather than impede it? I'm guessing that de Clercq would counter my criticism by saying he wants to be as thorough as possible, and that's why he included 19 pages of examples. And of course he needs to be thorough, and he certainly needs to demonstrate that thoroughness. Yet he could've written an economical four page article (instead of fourteen) with a substantial appendix that would both exhibit his meticulous research and analysis while also "tightening up" the essay by omitting the nonessential material. Though I regard the content of this article highly, I find the presentation problematic. In short, the content, while valuable, is not substantial enough to justify the verbose presentation. And so I return, once again, to "less is more": A more concise delivery would only make this essay better. The other day I received an email from a man named Brian Hebert. He recently published a book titled Blue Notes and Sad Chords: Color Coded Harmony in The Beatles 27 Number 1 Hits, and offered to mail me a complementary copy. I eagerly accepted Brian's offer, but countered by saying he could save shipping costs by just giving it to me in person. Since he lives in Massachusetts, and I'm speaking throughout the Bay State this month, why don't we meet in person to chat and exchange books? So we set up a meeting on Wednesday, July 18 at Stone's Public House in Ashland, MA. A splendid time was guaranteed for all! Indeed, the conversation was so engaging that an hour and half passed in what felt like ten minutes! Brian told me all about his experiences writing the book, and how he made various decisions. I happily chimed in with my own stories - good and bad - of whole process. We also conversed about several of the notoriously difficult chords to identify: the intro of 'A Hard Day's Night', the B chord (is it major? minor? is there a seventh?) in 'I Want To Hold Your Hand'. At one point during the meal, I asked Brian if he'd be interested in a blog interview to help promote the book. He heartily agreed, and I hope to publish that shortly. After generously picking up the check, Brian left the restaurant with my BEATLESTUDY, volume 1: Harmonic Analysis of Beatles Music in hand; I departed with Blue Notes. And I've been carefully reading it for the last several days. Below is my summary and review. The book is divided into three parts. The first section is introductory, establishing the basic premises for the book. “Hundreds of books in all sizes and shapes have been written about the Beatles,” Hebert writes. “Many are biographical … some books are primarily collections of photographs. Still other books help readers peer behind the curtains … A small number of books actually describe the music in detail [my emphasis]" [page 4]. An author after my own heart! He continues: “Typically written by musical experts, most of these books require the reader to possess a detailed understanding of music theory and a very specialized vocabulary, and as such are generally inaccessible to the average fan. … One goal of this book is to bridge that gap, and provide lovers of Beatles music with a unique and enjoyable way to understand some of the key musical elements that made the four lads from Liverpool so successful, without needing to be a musician or possess any specialized knowledge of music theory. … One of the key ideas this book hopefully gets across is that these musical concepts can be conveyed and understood intuitively, using relatively simple, color-rich graphics, which do not at all require an in-depth understanding of music theory” (pages 4, 6). Hebert makes it clear this is not an academic textbook, though it is analytic in nature: “This book is not intended as a scholarly work. You won't find footnotes or a list of references, and Wikipedia has been used as a main source for many facts” (page 12). The second section features color-coded “song map” textural analyses of The Beatles' 27 #1 hits (as included on the album 1), or in his own words, “the song maps show which Beatles are singing on the different parts of a song, and whether they are singing alone or together, in unison or in harmony” (page 3). In other words, the colors represent who is singing what. “If we assign a primary color to each singing Beatle voice (John red, Paul blue, and George yellow) and color code the parts of a song, we can see where they were singing alone, using a primary color, or together in unison or harmony, using secondary colors” (page 8). 'She Loves You' is a particularly vibrant example: Because the combinations of voices in this song are so varied (see the song map legend at the top right of the graphic), the song map's coloration is equally varied. The third and final section, for which the book is titled, analyzes harmony through a new color scheme, “using the analogy of an artist's palette of paints” (page 3). In this case, color represents not texture but harmony: red for I, green for ii, light gray for bIII, purple for iii, orange for IV, yellow for V, dark gray for bVI, light blue for vi, dark blue for bVII, and beige for vii. In general, brighter colors correspond to happier-sounding chords, where darker colors correspond to sadder-sounding chords. Here, for example, is the palette for 'Can't Buy Me Love': What this palette shows is that the verses employ the bright-sounding I (red), IV (orange), and V (yellow), while the refrains supplement with the dark-sounding iii (purple), and vi (blue). I've always found 'Can't Buy' fascinating for precisely this reason: The verses sound much happier than the refrains (what I would call choruses, but that's semantics and I won't get into it here). Furthermore, the lyrics reinforce this shift. In the darker-sounding refrains, the lyrics are negative, with Paul describing what cannot be done (“Can't buy me love...”). But in the brighter-sounding verses, the lyrics are more positive, describing what can be done (“I'll buy you a diamond ring...”, “I'll give you all I've got...”). Also, observant readers might notice a little blue dot in the above graphic, just to the right of the “V”. This indicates the use of a “blue note”, in which the pitch of a tone is lowered (ie, in a C major chord, the note E would be “normal”, while the note E-flat would be a “blue” note) for expressive reasons. “They can give a low-down, swampy, or lonesome feeling,” writes Hebert [page 17]. In the verses of 'Can't Buy', for instance, Paul frequently sings blue notes: “I'll buy you a dia-mond ring..”, “I'll get you a-ny-thing...”, “I'll give you all I got...”, “I may not have a lot...”, “Say you don't need no diamond rings...”, “Tell me that you want the kind of things...”. The Beatles (and a great many other pop musicians) use blue notes frequently. Where my own work (especially in the last year or two) has turned more analytic and technical, Hebert's Blue Notes and Sad Chords provides an accessible path for the obsessive but non-musician fan who wants to better understand the intricacies and sophistication of The Beatles' extraordinary music. And in addition to the colorful analytics, Hebert balances things out by including lots of non-technical nostalgic info, like calling out other artist’s songs in the charts before and after a Beatles hit, a back story for each number, personal memories and thoughts about the Beatles and the 1960s, and a condensed Beatles timeline. While I'm not a first-generation fan, I imagine the book could be a very pleasurable trip down memory (Penny?) lane for anybody that lived through the Sixties. As the book's back cover states: “Whether you're a long-time baby boomer Beatle fan, a younger newcomer, or somewhere in between, this book will give you an entirely new appreciation for the most amazing band ever.”
Blue Notes and Sad Chords is available for purchase on Amazon.com. The other day I blogged about my intent to "post summaries and reviews of articles and books by authors who have written about those 'purely musical achievements'." This will be the first such post. Mark Spicer is professor of music at Hunter College in New York, NY. He published an article in Music Theory Online last year in which he cites three examples of how pop musicians “toyed with tonality” by citing “three tonal scenarios”. This blog will summarize Spicer's main points and examples. I will close by relating his ideas to the catalog I know best: The Beatles. The first scenario Spicer considers are fragile tonics, which he defines as “the tonic chord is present but its hierarchical status is weakened”. Among other examples, Spicer cites Hall and Oates' 'She's Gone' (1973). The song is in E major, however the tonic chord is conspicuously absent from the verses, and appears only fleetingly (as a first-inversion passing chord on a week beat) in the choruses. This weakened tonic often corresponds to the lyrics, as is the case in Hall and Oates' 'She's Gone' (1973), in which the fragile tonic reflects the singer's fragile emotional state following a break-up: My face ain't looking any younger Now I can see love's taken her toll on me. She's gone. I 'd better learn how to face it. She's gone. I'd pay the devil to replace her. She's gone. What went wrong? The second tonal scenario are emergent tonics, in which “the tonic chord is initially absent yet deliberately saved for a triumphant arrival later”. Spicer cites Prince's 'Little Red Corvette' (1982) as an example. The tonic D-flat major chord, absent from the verses, emerges in the choruses, "where it serves as a metaphor for the release of the sexual tension built up in the preceding verse." Third are absent tonics, in which "the promised tonic chord never actually materializes.” Obviously this third category is the most difficult to discern for the reason that tonic is never heard - the song's harmony must convincingly imply tonic without actually giving it. From a compositional standpoint, this is tough to do (or at least it's difficult to do well); and from an analytic standpoint, it's heavily dependent on interpretation (how convincingly is tonic implied?). Spicer provides the example of 'Jane Says' (1988) by Jane's Addiction. The entire song consists of just two vacillating G and A chords, yet the song is clearly in D (judging from the sung melody). The tonic D major chord, then, is entirely absent - never heard, not even once, throughout the nearly-five-minute song. So there are Spicer's three categories of fragile, emergent, and absent tonics. How do The Beatles fit into these categories?
Well, the short answer is: They don't! The Beatles tend to be very clear about their tonics, and it's extremely rare to find a section of any given song (much less an entire song) with a fragile, emergent, or absent tonic. John Lennon's 'Glass Onion' (1968) is the sole exception. Lennon said about it: “I was just having a laugh, because there had been so much gobbledegook written about Sgt. Pepper. People were saying, 'Play it backwards while standing on your head, and you'll get a secret message.' … I threw the line in – 'The Walrus was Paul' – just to confuse everybody a bit more" (Dowlding, page 225; Sheff, page 208). So the lyrics aren't supposed to make sense! And indeed, the harmony (appropriately) doesn't make sense, either. In BEATLESTUDY, I analyzed it three different ways: in C major, in A minor, and in F major. None of those three fit perfectly, but between the three I think I covered it pretty well. The only cadences in 'Glass Onion' are the g-C-F progressions (ii-V-I in F major) heard from 0:15-0:19, 0:44-0:49, and 1:34-1:38; and the F-G-a progressions (bVI-bVII-i in A minor) heard from 0:27-0:31, 0:57-1:01, and 1:16-1:20. But if I had to pick "the best tonal interpretation", I'd probably chose C major, even though there are no cadences to confirm that tonality. In fact, every time a potential cadence builds (every time we hear a strong predominant followed by a strong dominant), that expectation is thwarted by meandering harmony. So I think the best interpretation of 'Glass Onion' is with the absent tonic of C major. REFERENCES
|
Aaron Krerowicz, pop music scholarAn informal but highly analytic study of popular music. Archives
August 2019
Categories
All
|
||||||||||||||||||||||||||||||||||||||







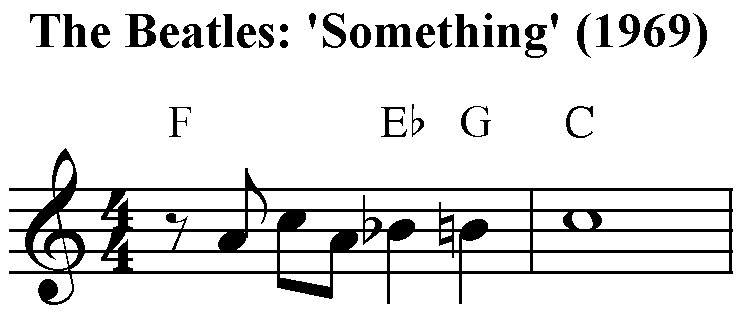





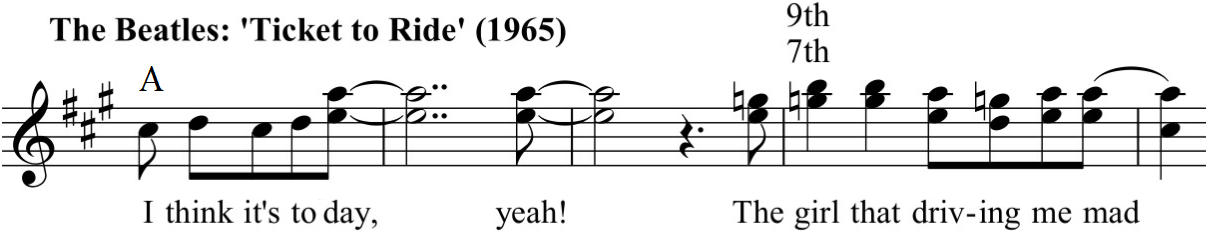
















 RSS Feed
RSS Feed
